Neural Networks

Building Blocks

Gradient Descent

finding the optimum in parameter space

Strategies:

Batch: $\theta = \theta - \eta \cdot \nabla_ \theta J(\theta)$
Stochastic: $\theta = \theta - \eta \cdot \nabla_\theta J(\theta;x_i;y_i)$, faster but biased
Mini-batch: $\theta = \theta - \eta \cdot \nabla_\theta J(\theta;x_{i:i+m};y_{i:i+m})$, intermediate

Challenges:

$\eta$: apply learning rate schedules
Saddle points as local minimum: spiking NN for quantum tunneling?

Improvements for SDG:

add momentum: $v_t = \gamma v_t - 1 + \eta \cdot \nabla_\theta J(\theta); \theta = \theta -v_t$, reduce damping
NAG, Nesterov accelerated gradient: add correction based on momentum, $J(\theta) -> J(\theta - \gamma v_t - 1)$, avoid momentum crash
Adagrad, adaptive gradient: $\eta_i$ for each $\theta_i$, $\theta_{t+1}=\theta_t - \frac{\eta}{\sqrt{G_t+\epsilon}}\odot g_t$
Adadelta: reduce the calculation of $G_t$ with a window-based average, $E_t$
RMSprop: $E_t = \gamma E_{t-1} + (1-\gamma)g_t^2$
Adam, adaptive moment estimation: bias-corrected from weighted average mean and variance

Asynchronous SGD for parallelization:

Hogwild
Downpour SGD
Delay-tolerant Algorithms for SGD
TensorFlow
EASGD, elastic Averaging SGD: local variable fluctuate from center variable

Extra to explore:

Shuffling and Curriculum Learning
Batch normalization: keep N(0,1)
Early stopping: avoid overfitting
Gradient noise: shuffle away from local

Overview of Gradient Descent refs

Activation Function

back-propagatable, non-linear projection

keep nonlinearity & non-vanishing gradient

Sigmoid: $f(x) = \frac{1}{1 + e^{-x}}$, work with cross-entropy cost function $y\ln{a}+(1-y)\ln{(1-a)}$ to avoid gradient vanishing
tanh, $tanh(x)= 2 \sigmoid(2x)-1$: better but not the final solution
ReLU, $y=x\ge0? x:0$
- constant gradient on one side
- output shift & hard to converge
PReLU, $f(y_i)= y_i>0? y_i: a_iy_i$: regulate the left side
- He, K., et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. ICCV 2015
- RReLU, Xu, B., et al. Empirical Evaluation of Rectified Activations in Convolutional Network. ICML Deep Learning Workshop 2015
Maxout, $\max{w_ix+b_i}$
ELU, $f(x)= x>0?x:\alpha (\exp(x)-1)$
- ImageNet example
Noisy Activation Functions, Gulcehre, C., et al., Noisy Activation Functions, in ICML 2016. 2016
CReLU, pair-grouping phenomenon
MPELU

Practical tips:

ReLU
ELU
PReLU/MPELU with regularizer/penalty

Regularization

minimize the loss function with reasonable complexity

Supervised learning: $w^* = \arg\min_w \sum_i L(y_i, f(x_i;w)) + \lambda \Omega(w)$, solve ill-conditioned matrix

L0/L1, minimize the absolute sum: Lasso regularization, make $w$ sparse, $||w||_1 \le C$, linear bound

Feature Selection: less feature needed
Interpretability: less complex

less features

L2, minimize the square sum: Ridge Regression/Weight Decay, $||w||_2 \le C$, quadratic bound

won't reduce features
but reduce certain feature dependence

Tuning Methods

the evil approach

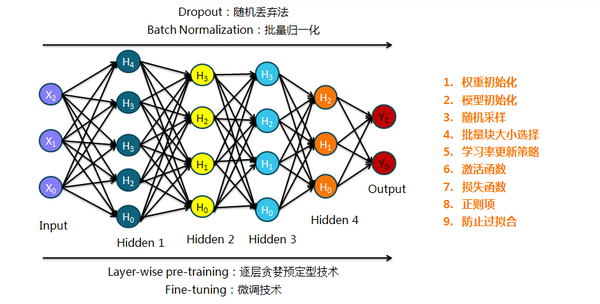
Neural Networks

Feedforward Neural Network: word2vec
- Huffman tree
- CBOW: words -> word
- skip-gram: word -> words
Denoising Autoencoders: obtain good representation
- perform noise mapping: $x \rightarrow \tilde{ x}$
- keep loss as $\mathcal{L}(x,\tilde{x'})$
Restricted Boltzmann Machine: unsupervised learning
- generative approach: obtain $P(X,Y)$ for P(Y|X); in contrast of discriminative approach, which only cares about $P(Y|X)$
  - methods: Markov process & Gibbs sampling
  - metrics: KL divergence, Shannon entropy, $\sum_i P(i)\log\frac{P(i)}{Q(i)}$
- probability distribution: $P = \frac{1}{Z}e^{-E(v,h)}$
- energy function: $E(v,h) =-v^T Wh -a^Tv -b^Th$, $v$ visible unit, $h$ hidden unit
Generative Adversarial Network: Turing learning
- discriminator: convolutional
- generator: deconvolutional
- applications
  - synthesis face from text: progressive growing of GANs, training method
  - recover features in astrophysical images of galaxies beyond the deconvolution limit
  - EnhanceNet: Single Image Super-Resolution Through Automated Texture Synthesis
  - generating images in latent space
Residual Neural Network
- plain layer + shortcuts
- residual function: $\mathcal{F}(x):=h(x) - x$
- shortcut: $y=w_s x + \mathcal{F}(x, {w_i})$
Convolutional Neural Network: computer vision
- convolutional layer with kernels
Recurrent Neural Network
- LSTM: a memory cell $c_t$, an input gate $i_t$, an 'output' gate $o_t$ and a forget gate $f_t$. $x_t \rightarrow h_t$
- Attention: potential of memory
- applications
  - Semantic MEDLINE: MEDLINE intelligence, NLP on medical papers
  - ORiGAMI: term weight and so on
  - Acoustic modeling: ASR
  - Image description

Spiking Neural Network (3rd generation)

Spiking neuron: accumulate their activation into a potential over time, and only send out a signal (a "spike") when this potential crosses a threshold and the neuron is reset.

Integrator: memory or nonlinear response